Am 31.01.2013: Dipl.-Math. F.Hermann: "Die geschlossenen Mannigfaltigkeiten. Gestern und heute."

Was ist die geschlossene Mannigfaltigkeit? Wir kommen zur Bestimmung der geschlossenen Mannigfaltigkeit mit der strengen mathematischen Formulierung nicht heran, sondern beschränken uns auf die intuitive Beschreibung dieses Begriffes.

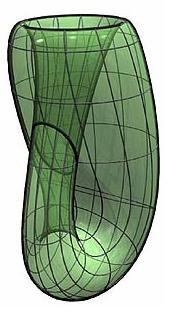
Die einfachste triviale geschlossene Mannigfaltigkeit der Dimension n=1 ist der Kreis. Jeder Kreis wird mit dem Radius charakterisiert. Wenn der Radius gleich Null ist, so bekommen wir die einfachste geschlossene Mannigfaltigkeit der Nulldimension (den Punkt). Die einfachste geschlossene Mannigfaltigkeit der Dimension n=2 ist die Sphäre. Wir kennen eine solche Figur als Torus („Rettungsring“, „Donuts“). In der Topologie wird der Torus als die Multiplizierung von zwei Mannigfaltigkeiten der kleineren Dimensionen dargestellt. Die bekannte kleinsche Flasche ist auch eine geschlossene Mannigfaltigkeit. Aber bei der kleinschen Flasche erscheint schon die neue Charakteristik. Wenn die Sphäre und der Torus die Mannigfaltigkeiten sind, auf die man eine Orientierung geben kann, so ist die kleinsche Flasche eine nicht-orientierbare Mannigfaltigkeit.

Die einfachste nicht triviale geschlossene Mannigfaltigkeit ist die projektive Ebene. Gibt es hier keinen Gegensatz? Anscheinend handelt es sich um die Ebene, aber gleichzeitig ist diese Ebene geschlossen. Es handelt sich darum, dass jede Gerade von projektiven Ebenen im Unterschied zu euklidischen Ebenen den unendlich entfernten Punkt hat. Wenn wir auf irgendeiner willkürlichen Geraden einer projektiven Ebene einen willkürlichen Punkt nehmen und beginnen uns von ihm in verschiedene Richtungen wegzubewegen, so werden wir uns in einem unendlich entfernten Punkt auf jeden Fall treffen. Alle unendlich entfernten Punkte liegen auf einer unendlich entfernten Geraden. In unserem alltäglichen Verständnis für die Weise der unendlich entfernten Geraden kann man die Linie des Horizontes übernehmen, die man in der Steppe oder auf dem Meer gut beobachten kann.

Die projektive Ebene, wie die geschlossene Mannigfaltigkeit, hat viele interessante Eigenschaften, die wahrscheinlich schon immer die Aufmerksamkeit der Mathematiker und , in letzter Zeit, der Physiker auf sich zog. Jetzt etwas über diese Eigenschaften:

Den Begriff des Koordinatensystems auf der projektiven Ebene kann man auf verschiedene Weise einführen, dabei fehlt der Punkt des Anfanges der Koordinaten auf der projektiven Ebene. Dieser Punkt gehört immer zu dem Raum, dessen Dimension auf eine Einheit größer ist als die Dimension jenes Raumes, wo das Koordinatensystem eingeführt wird.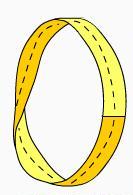

Die projektiven Räume der geraden Dimension sind immer die Räume, auf denen es unmöglich ist, die Orientierung einzuführen. Mit anderen Worten heißt das : man kann auf der projektiven Ebene immer die einseitige Oberfläche wählen, die wir das Möbiusband nennen. Und die axiale Linie des Möbiusbands ist ein Abbild der Geraden der projektiven Ebene.

Jeder Punkt und jede Gerade werden mittels dreier Koordinaten vorgegeben. Von der mathematischen Darstellung der Punkte und der Geraden ist es unmöglich ohne zusätzliche Erklärungen zu verstehen, worum es sich handelt, um die Punkte oder um die Geraden. Diese Eigenschaft heißt das Prinzip der Dualität.

Außerdem kann man sagen, dass eine projektive Ebene mehr als Zehn verschiedene mathematische Modelle hat, was zusätzliche Möglichkeiten für ihr Studium (Forschung) gibt.

Man muss besonders bemerken, dass projektive Geometrie als Ausgangsprototyp für die Konstruktion überhaupt einer beliebigen Geometrie, wie euklidischer als auch nichteuklidischer, dienen kann.

Dipl.-Math. F.Hermann